2192: 【入门】哈夫曼树(2)
时间限制: 1 Sec 内存限制: 128 MB提交: 0 解决: 0 金币: 1
[提交][状态]
题目描述
哈夫曼树的定义是:一棵具有n个带权叶结点的二叉树,是的所有叶结点的带权路径长度(叶结点×叶结点到根结点的路径长度)之和最小,这样的二叉树被称为最优二叉树,也称哈夫曼树。
比如:有4个结点的权值是5 4 2 9,可以构建出如下三颗不同的二叉树,第2棵二叉树的带权路径长度是最小的。
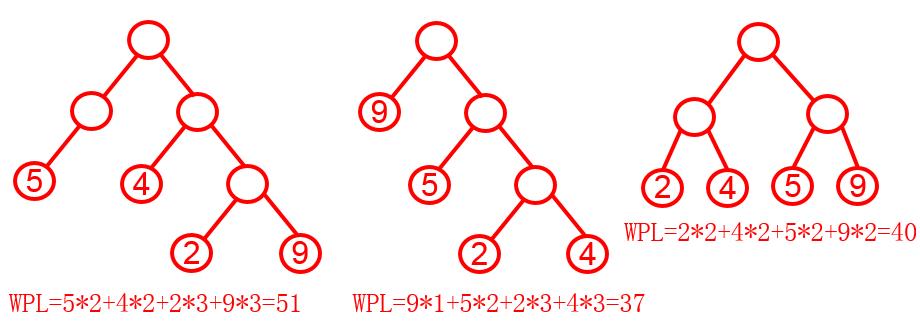
请读入一个整数n,代表叶结点的数量,再读入n个整数,代表叶结点的权值,请求出对应哈夫曼树的带权路径长度。
输入
第1行有一个整数m(m≤20),表示有m组测试数据。
每组第一行输入一个数n,接着输入n个叶节点的权值(叶节点权值不超过100,2<=n<=1000)。
输出
输出每组数据对应哈夫曼树的带权路径长度,每行一个。
样例输入复制
2
2
2 8
3
5 11 30
样例输出复制
10
62